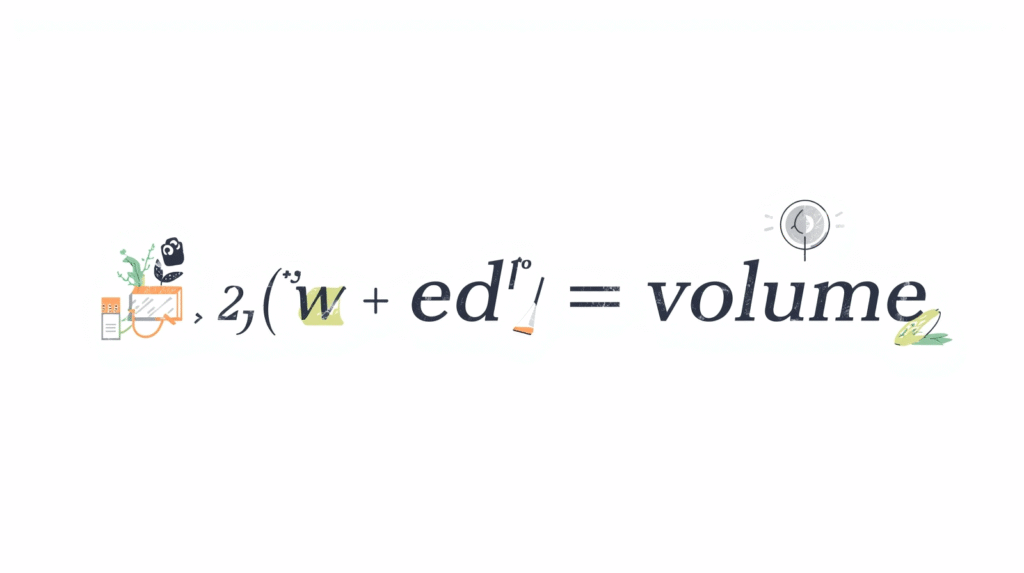Understanding how to find the volume of different shapes is a super helpful skill. Whether you’re filling up a box, measuring water in a pool, or learning math at school, the formula for volume helps you know how much space something takes up. Don’t worry — this guide will make it simple, fun, and easy to follow.
Let’s explore how to calculate the volume of all kinds of shapes step by step. You’ll also see real-life examples, clear formulas, and some handy tips to help you remember everything.
Table of Contents
What Is Volume?
Volume is the amount of space an object takes up. Imagine pouring water into a box — the amount of water that fits inside shows the volume of that box. In simple words, it tells us how much stuff can fit inside something.
We measure volume in cubic units because it’s a measure of three-dimensional space. For example, you might see measurements like cubic centimeters (cm³), cubic meters (m³), or liters (L).
Whenever you see a 3D object — a ball, a cup, or even a swimming pool — it has volume. The formula for volume helps you find that exact amount quickly.
Why Knowing the Formula for Volume Is Important
Learning the formula for volume isn’t just about passing a math test. It’s something you can use every day!
Think about these situations:
- You want to fill a box with toys — knowing the volume tells you how much it can hold.
- A farmer wants to store grain in a silo — the formula for volume helps them find capacity.
- Engineers and architects use volume to design buildings and rooms.
- Even when cooking or filling a tank, you use the concept of volume without realizing it.
Understanding this formula gives you a better idea of how things fit together in real life.
Basic Formula for Volume
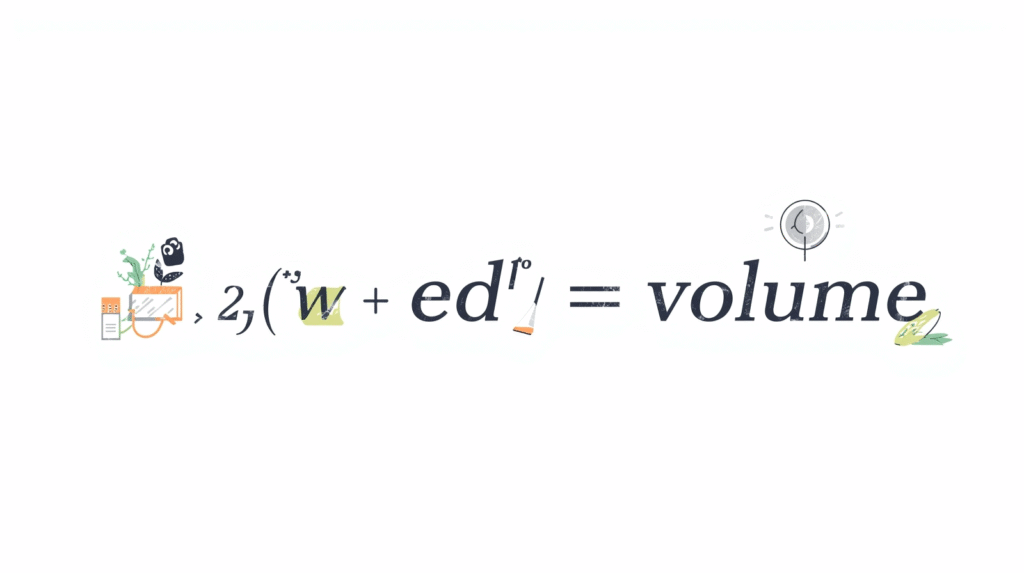
The general formula for volume depends on the shape. But the basic idea stays the same — you multiply the space along three dimensions: length, width, and height.
For most box-like shapes, the simple formula is:
Volume = Length × Width × Height
That’s it! If you know how long, wide, and tall an object is, just multiply those numbers together. The answer tells you how much space the object takes up.
Formula for Volume of a Cube
A cube is a 3D square — all sides are equal. So instead of length, width, and height, you just need one measurement: the side.
Volume of a Cube = Side × Side × Side
or V = a³
Example:
If one side of a cube is 4 cm,
V = 4 × 4 × 4 = 64 cm³.
So the cube’s volume is 64 cubic centimeters. Easy, right?
The formula for volume of a cube is one of the simplest, and it’s a great place to start.
Formula for Volume of a Rectangular Prism
A rectangular prism looks like a box or a brick. Unlike a cube, its sides can have different lengths.
Volume = Length × Width × Height
Example:
If a box is 10 cm long, 5 cm wide, and 4 cm tall:
V = 10 × 5 × 4 = 200 cm³
That means the box can hold 200 cubic centimeters of space.
You’ll see this formula for volume used all the time — from packaging design to shipping containers.
Formula for Volume of a Cylinder
A cylinder looks like a can or a tube. To find its volume, you need the radius of its circular base and its height.
Volume = π × r² × h
Here, π (pi) is about 3.1416, r is the radius, and h is the height.
Example:
If the radius is 3 cm and the height is 10 cm:
V = 3.1416 × 3² × 10 = 3.1416 × 9 × 10 = 282.74 cm³
The formula for volume of a cylinder helps you find how much liquid or material fits inside objects like cans or pipes.
Formula for Volume of a Cone
A cone is like an ice cream cone or a traffic cone — wide at the base, narrow at the top.
Volume = (1/3) × π × r² × h
The “one-third” in the formula means a cone holds one-third the volume of a cylinder with the same base and height.
Example:
If a cone has a radius of 4 cm and height of 9 cm:
V = (1/3) × 3.1416 × 4² × 9 = (1/3) × 3.1416 × 16 × 9 = 150.8 cm³
So the cone’s volume is 150.8 cubic centimeters.
Formula for Volume of a Sphere
A sphere is a perfect ball — like a basketball or a bubble. To find its volume, you just need the radius.
Volume = (4/3) × π × r³
Example:
If the radius is 5 cm,
V = (4/3) × 3.1416 × 5³ = (4/3) × 3.1416 × 125 = 523.6 cm³
The formula for volume of a sphere is useful in sports, physics, and even astronomy when measuring planets or bubbles!
Formula for Volume of a Pyramid
A pyramid has a polygon base (often square) and comes to a point at the top. Its volume formula is similar to a cone’s:
Volume = (1/3) × Base Area × Height
Example:
If the base is a 6 cm × 6 cm square and the height is 9 cm:
V = (1/3) × (6 × 6) × 9 = (1/3) × 36 × 9 = 108 cm³
So the volume of the pyramid is 108 cubic centimeters.
Formula for Volume of an Irregular Object
Not everything has a neat shape! What if you want to know the volume of a rock or toy car?
You can use water displacement:
- Fill a measuring cup with water and note the level.
- Submerge the object completely.
- Measure the new water level.
- Subtract the first number from the second — that’s the volume of the object!
This simple method works for all kinds of irregular shapes and gives an accurate measure of volume in milliliters or cubic centimeters.
Real-Life Examples of Using the Formula for Volume
Here are a few everyday ways we use volume without realizing it:
- Cooking: Measuring ingredients like oil or milk.
- Building: Calculating how much concrete fits in a mold.
- Shipping: Knowing how many boxes fit in a truck.
- Science: Measuring how much gas or liquid fits in a container.
- Gardening: Estimating soil needed for a planter.
In every case, understanding the formula for volume helps you save time, materials, and effort.
Common Mistakes When Using the Formula for Volume
Even simple math can be tricky sometimes! Here are a few mistakes to watch for:
- Mixing units — Don’t multiply centimeters by meters. Keep units consistent.
- Forgetting π — Always use 3.1416 (or the π button on a calculator) for circular shapes.
- Wrong measurements — Measure the radius (not diameter) when working with circles.
- Missing one dimension — Always include length, width, and height when needed.
Being careful with these small details keeps your answers accurate every time.
Fun Facts About Volume
- The word volume comes from Latin volumen, meaning “roll” or “something that occupies space.”
- A sphere has the largest volume for the smallest surface area — that’s why bubbles are round!
- NASA engineers use volume formulas when designing rocket fuel tanks.
- The average human body has a volume of about 66 liters!
Pretty cool, right? Understanding the formula for volume helps you see math in the real world around you.
Tips to Remember the Formulas
Here are a few tricks to help you remember the formulas easily:
- Cube and box: Multiply all three sides.
- Cylinder: Circle area × height.
- Cone and pyramid: Cylinder or box volume ÷ 3.
- Sphere: Multiply radius cubed by 4/3π.
Write them down, draw diagrams, or use 3D models to help your brain remember better. Repetition makes it stick!
Frequently Asked Questions (FAQs)
1. What is the easiest formula for volume?
The easiest is the box formula: Volume = Length × Width × Height. It works for cubes and rectangular prisms.
2. Why do we use cubic units for volume?
Because volume measures space in three dimensions, so we multiply three lengths — giving us cubic units (like cm³).
3. How do I find the volume of a cylinder?
Use π × r² × h, where r is radius and h is height. Don’t forget π = 3.1416.
4. Can I find volume without a formula?
Yes! For irregular shapes, use water displacement — it’s accurate and simple.
5. What’s the difference between area and volume?
Area measures surface (2D), while volume measures space inside (3D).
6. How can I practice finding volume?
Use real objects at home — boxes, cans, or balls. Measure them and apply the correct formula for volume to check your answers.
Conclusion
Volume is all around us — in boxes, bottles, and buildings. The formula for volume helps us understand how much space things occupy and how much they can hold.
By learning these formulas and practicing with real examples, you’ll see math isn’t just numbers — it’s a tool to understand the world better. Whether you’re a student, builder, or just curious, mastering the formula for volume makes life a little easier and a lot more fun.
So next time you look at a box, a cup, or even a planet, you’ll know exactly how to figure out its volume. Pretty amazing, right?