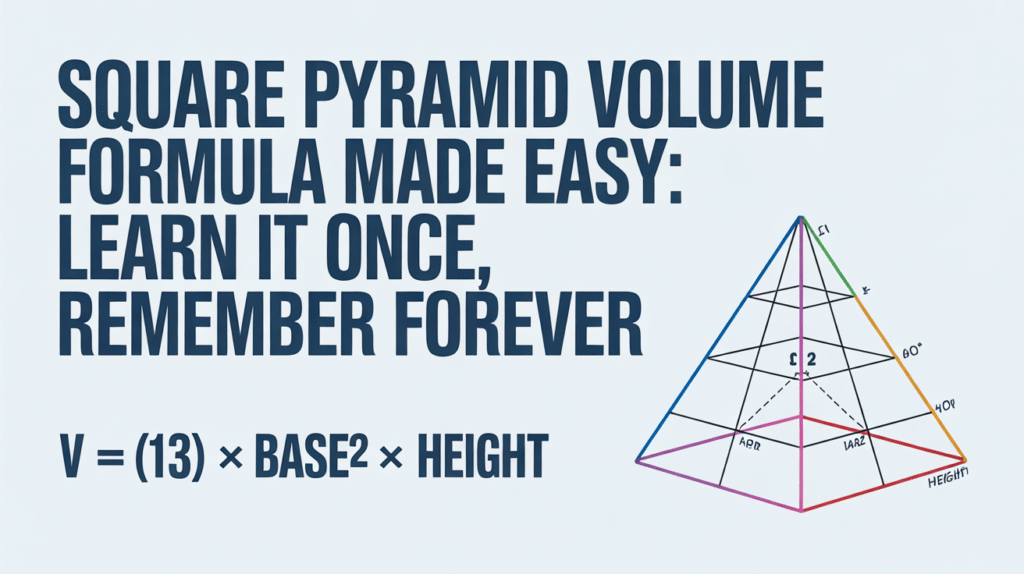I love shapes, and I love clear math. This piece will explain the square pyramid volume formula step by step. I will use simple words and short sentences. You will learn what each part of the formula means. You will see examples you can try. I will give tips to avoid common mistakes. The tone is friendly and plain. You will feel able to solve problems after reading. I promise no heavy math words without an explanation. This article also gives practice problems. You will get answers and short explanations. Let’s make geometry easy and fun. Ready? Let’s start with the basics and the main idea behind the formula.
Table of Contents
What is a square pyramid?
A square pyramid is a solid. Its base is a square. Four triangular faces meet at a single point. That top point is the apex. The base side is often called s. The vertical distance from the base to the apex is the height. People call that height h. The square base and the height are the two needed parts for volume. Not the slant height. The slant height helps with the surface area. But for volume, you only need the area of the square base and the height. This shape looks like the Egyptian pyramids. It also appears in many math problems and models.
The simple statement of the square pyramid volume formula
The square pyramid volume formula is short and neat. It says: Volume = (1/3) × base area × height. For a square base, base area is s². So the formula becomes V = (1/3) × s² × h. You multiply the square of the side by the height. Then you divide by three. The 1/3 factor is important. It makes the pyramid smaller than a prism with the same base and height. This formula gives the space inside the pyramid. Use the same units for s and h. The result is in cubic units.
Why the formula has one third
The one third in the square pyramid volume formula needs explanation. Imagine a prism with the same base and height as the pyramid. The prism is like a tall box. Its volume is base area times height. A pyramid with the same base and height takes one third of that space. You can show this with many small cubes or with calculus in higher math. A classic proof uses slicing or stacking methods. For children, simple models help. Cut a prism into three equal pyramids in a model. Each pyramid will have the same base and height and one third of the prism’s volume. That is why the 1/3 appears in the formula.
Parts of the formula explained: base area
In the square pyramid volume formula, base area matters. For a square, base area equals side length squared. If the side is s, the area is s². That means s multiplied by s. Use the same unit for both sides. If s is in meters, s² is in square meters. The base area tells how wide the shape is. A larger base leads to a larger volume, all else equal. You can measure the base on a model or from a drawing. Keep units straight. If you convert units, do so before squaring the side length.
Parts of the formula explained: height
The height in the square pyramid volume formula is the straight, vertical distance. It goes from the base plane to the apex. It is not the slanted side of the pyramid. If the apex is not directly above the center, the height is still the shortest connection from the base plane to the apex. For right square pyramids, the apex lies above the center. That makes measuring height easier. Always measure height in the same unit as the base side. If you measure in centimeters, convert other measures to centimeters too. Height enters the formula linearly. Doubling height doubles volume, if base area stays the same.
How to use the formula step by step
First, measure the side length s of the square base. Second, calculate the base area by squaring s. Third, measure the height h. Fourth, plug into the square pyramid volume formula: V = (1/3) × s² × h. Fifth, do the multiplication then divide by three. Sixth, label your answer with cubic units. Follow order: square, multiply, divide. Example: s = 4 units, h = 9 units. Base area = 4² = 16. Multiply by h: 16 × 9 = 144. Divide by 3: 144 ÷ 3 = 48. Volume = 48 cubic units. That shows the steps clearly.
Example 1 — simple numbers
Let’s try a quick example using the formula. Suppose s = 3 centimeters. The height h = 6 centimeters. First find base area: s² = 3² = 9 cm². Now use the square pyramid volume formula: V = (1/3) × 9 × 6. Multiply 9 by 6 to get 54. Now divide by 3 to get 18. The volume is 18 cubic centimeters. You can picture 18 little 1 cm cubes filling the pyramid. This hands-on view makes the formula real. Start with small integers for practice. It makes the steps easy to check.
Example 2 — a larger example with decimals
Try s = 4.5 meters and h = 10 meters. First square the side: 4.5 × 4.5 = 20.25 m². Now use the square pyramid volume formula: V = (1/3) × 20.25 × 10. Multiply area by height: 20.25 × 10 = 202.5. Divide by 3 to get 67.5. The volume is 67.5 cubic meters. Make sure your calculator uses the same units. Note how decimals work the same as whole numbers. The one third still reduces the prism volume by a third.
What if you know diagonal or base area directly
Sometimes you do not know the side but you know the base area. That is fine. The square pyramid volume formula works with base area A. Use V = (1/3) × A × h. If you know the diagonal d of the square base, you can get s from d. For a square, diagonal d = s√2. So s = d ÷ √2. Then square s to find base area. Use the units carefully. This flexibility helps in problems. You never need the slant height to find volume. The formula stays simple with area and height.
Units and real-world meaning
The square pyramid volume formula gives cubic units. If s and h are in inches, the volume is in cubic inches. If they are in meters, the volume is in cubic meters. Units tell you the real-world size. For small models, the volume tells how much space inside the pyramid is available. For big structures, the formula tells how much material might fit inside. Always write units with your answer. That helps avoid mistakes. If you convert one measure from centimeters to meters, convert the other too. Units can be scaled easily.
Common mistakes and how to avoid them
Students often use slant height by mistake. Slant height is not the same as height. Slant height is the length of a triangular face from base to apex along the face. Another mistake is forgetting to square the side. Also watch units. A final slip is forgetting the one third. To avoid errors, write each step. Label numbers carefully. Sketch the pyramid and mark s and h. Use a different color for the height. Check if the apex is directly above the center. If not, the basic right pyramid formula still needs height, but the figure may be more complex.
Comparing to a triangular pyramid
A triangular pyramid has a triangular base. Its volume uses a similar idea. Volume = (1/3) × area of triangular base × height. The square pyramid volume formula is a special case where the base is a square. The factor of one third is common for pyramids. This shows a family connection. For both shapes, base area and height determine volume. The shape of the base only changes how you compute the base area. That similarity makes learning one formula help with others.
How the formula works visually (stacking idea)
A visual way to see the square pyramid volume formula is to think of layers. Slice the pyramid horizontally into very thin layers. Each slice is a small square. Their areas change as you move up. Add up the volumes of all thin layers. The sum equals the full volume. In math, this process is integration. But at a school level you can think of many thin sheets stacked. The sum of these sheet volumes equals one third of a prism with the same base and height. This mental model helps. It gives intuition behind the one third factor in the square pyramid volume formula.
Real-world examples where volume matters
Architects and engineers sometimes need pyramid volumes. Gardeners might build pyramid planters. Toy designers use pyramid shapes for pieces. Even video game designers use pyramid-like meshes. The square pyramid volume formula helps plan materials and space. If you make a small decorative pyramid, you can find how much wood to hollow it out. If you plan a sandbox with pyramid sides, you can estimate sand needed. These are ordinary tasks where simple math helps. The formula saves time and prevents waste.
Using the formula in word problems
Word problems often hide s and h inside sentences. Read carefully to find which numbers are side lengths and which are heights. Sometimes the problem gives the area of the base already. Sometimes it gives volume and asks for height. If you know volume, rearrange the square pyramid volume formula to solve for missing values. For height, h = 3V ÷ s². For side, s = √(3V ÷ h). Always isolate the unknown and solve step by step. Show units and box the final answer.
Rearranging the formula to find height or side
If you know volume and side, you can find height. Start with square pyramid volume formula: V = (1/3) × s² × h. Multiply both sides by 3 to get 3V = s² × h. Divide by s² to get h = 3V ÷ s². If you know volume and height, find side by rearranging: s² = 3V ÷ h. Then s = √(3V ÷ h). Use a calculator for the square root. Keep units in mind, because s will be in the same length unit as h. These reversible steps help solve a range of problems.
Slant height and surface area vs volume
Slant height matters for surface area. The slant height is the length from the base edge up the face to the apex. Surface area adds the area of the base and the area of the four triangular faces. That calculation uses slant height. Volume uses the vertical height only. Do not mix them. A common exam question asks for both volume and surface area. Measure slant height l, base side s, and height h separately. The triangular face area of each triangle is (1/2) × s × l. There are four such faces for a square pyramid.
Simple proof idea for curious learners
A simple proof of the square pyramid volume formula uses cubes or stacking. Imagine building the prism with tiny cubes. Then try to group cubes to form three identical pyramids. Each pyramid will match the base and height. This visual shows the prism is three times the pyramid. Another proof slices the prism and pyramid and compares areas of cross-sections. While calculus offers rigorous proofs, the stacking idea gives a strong geometric intuition. Teachers often use physical models to demonstrate this proof.
Scaling and how size affects volume
If you scale all lengths by a factor k, volume changes by k³. For a square pyramid, scaling side and height by k multiplies volume by k³. For example, double side and height. The new volume is eight times bigger. That is because area scales by k² and height scales by k. The square pyramid volume formula shows the cube relationship clearly. This idea helps predict how big objects grow when scaled. It also helps with models and printing, so that you can estimate material use.
Practice problems for confidence
Practice helps a lot. Problem 1: s = 2 cm, h = 6 cm. Find volume. Problem 2: s = 5 in, h = 12 in. Find volume. Problem 3: Volume is 160 cubic meters; s = 8 m. Find h. Problem 4: h = 15 cm and volume is 225 cm³. Find s. Work each problem with the square pyramid volume formula. Show steps. Check units. For problem 3 use h = 3V ÷ s². These examples will anchor the concept in your mind. Try more with decimals to improve fluency.
Answers to practice problems
Answers come after working each step. Problem 1: base area = 2² = 4; V = (1/3) × 4 × 6 = 8. Volume = 8 cm³. Problem 2: base area = 25; V = (1/3) × 25 × 12 = 100. Volume = 100 in³. Problem 3: h = 3V ÷ s² = 3×160 ÷ 64 = 480 ÷ 64 = 7.5 m. Problem 4: s² = 3V ÷ h = 3×225 ÷ 15 = 675 ÷ 15 = 45. So s = √45 ≈ 6.708 cm. Use a calculator for the square root. These worked answers help you check your method.
Tips for tests and homework
Write units with each number. Show all steps. If the problem gives base area directly, use V = (1/3) × A × h. If the apex is not centered, draw a clear picture and mark the true height. Keep a ruler handy for diagrams. Check if the problem asks for rounding. Use at least two decimal places when needed. If the question uses a formula sheet, compare your steps. Small arithmetic errors cause the most trouble. Slow down and double-check calculations.
Teaching kids the idea with hands-on activities
Children learn geometry with hands-on play. Build a small paper square pyramid. Use cardboard or paper to make a net. Fill it with rice to see volume. Measure rice with a small cup of known volume. Compare with a small box (prism) of the same base and height. Notice how the pyramid needs less rice. These activities make the square pyramid volume formula memorable. They also show the one third factor visually. Keep activities short and fun. Let kids draw and explain back what they saw.
Advanced note: calculus perspective (brief)
For older students, calculus explains the square pyramid volume formula neatly. You can slice the pyramid into thin horizontal sheets. Each sheet has area proportional to the square of its distance from the apex. Integrating these areas along the height gives the total volume. The result of the integral is one third times base area times height. This matches the square pyramid volume formula we used. The calculus approach is more formal. It is useful when you study more complex solids later.
Common classroom questions answered
Students often ask: “Why not one quarter or one half?” The answer is in geometric comparisons to prisms and through slicing arguments. Another question: “Do we need slant height?” Not for volume, only for surface area. People also ask about non-right pyramids. The formula still works if you use the vertical height. In tilted pyramids, measure the perpendicular height. These quick answers help reduce confusion during class.
Summary of key points
The square pyramid volume formula is V = (1/3) × s² × h. Use s for the base side and h for the vertical height. Square the side to get base area. Multiply by height. Divide by three. Keep units consistent. Do not use slant height in the formula. You can rearrange the formula to find missing values. This formula links to many practical and test situations. Practicing examples builds confidence. Remember visual models to see why the one third appears.
Conclusion
You now know how to use the square pyramid volume formula. Try drawing and solving three new problems. Build one small model with paper or cardboard if you can. Teach a friend or family member how to use the formula. Teaching helps you remember. Share one practical use you found. If you have a question, ask it and I will help you solve it step by step. Keep practicing and use the steps shown here. Geometry becomes easier with simple habits and clear diagrams.
Frequently Asked Questions (FAQs)
FAQ 1: What is the square pyramid volume formula and when do I use it?
The square pyramid volume formula is V = (1/3) × s² × h. Use it when the base is a square. The formula needs the base side s and the vertical height h. Use it for right or tilted pyramids if you know the perpendicular height. It tells the space inside the pyramid in cubic units. Remember the base area is s² and the one third factor makes the volume smaller than a prism with same base and height.
FAQ 2: Can I use slant height in the square pyramid volume formula?
No. The slant height is not part of the square pyramid volume formula. Slant height helps find the surface area of triangular faces. For volume, you must use the vertical height. If you only know slant height, you might use the Pythagorean theorem to find the vertical height. That works when the apex is centered above the base.
FAQ 3: How do I find height if I know the volume and side?
Rearrange the formula. Start with V = (1/3) × s² × h. Multiply both sides by 3 to get 3V = s² × h. Then divide by s² to get h = 3V ÷ s². Make sure to use the same units for s and h. This gives the perpendicular height directly.
FAQ 4: What units will the answer use?
The answer will use cubic units. If side s and height h are in centimeters, the volume is in cubic centimeters. If they are in meters, the volume is in cubic meters. Always label your final answer with cubic units. Convert units before computing if they differ.
FAQ 5: Why is the factor one third in the formula?
The one third comes from geometry. A pyramid uses one third of the space of a prism with the same base and height. You can see this by stacking or slicing models. The factor appears the same for all pyramid bases. It is a core geometric fact proven by slicing or by calculus.
FAQ 6: Does the formula work for any pyramid base shape?
Yes, but the formula form changes for non-square bases. In general, volume = (1/3) × base area × height. For a square base, base area is s². For a triangular base, base area is (1/2) × base × height. Once you know base area, the one third times base area times vertical height always gives the pyramid volume.