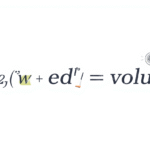Have you ever wondered how to find the Triangular Prism Volume? Don’t worry—it’s much easier than it sounds! In this guide, we’ll explore what a triangular prism is, why it matters, and how to calculate its volume using simple steps. By the end, you’ll be a pro at solving any prism volume problem.
Whether you’re a student, teacher, or just someone who loves learning, this guide will walk you through everything in an easy, friendly way. You’ll also find real-life examples, tips, and answers to common questions. Let’s dive right in and make math fun!
Table of Contents
What Is a Triangular Prism?
A triangular prism is a three-dimensional (3D) shape with two identical triangles on opposite ends. These triangles are connected by three rectangular faces, forming a solid object. Think of it like a tent, a Toblerone chocolate bar, or the roof of a house.
The two triangles are called bases, and the rectangles connecting them are called lateral faces. Together, they create a prism shape that can hold space inside. That’s where the concept of volume comes in—volume measures how much space the prism takes up.
Understanding the Concept of Volume
Volume tells us how much space a 3D object occupies. In other words, it’s the amount of “stuff” that could fit inside it. For example, if you could fill a triangular prism with water, the volume would tell you exactly how much water it could hold.
We usually measure volume in cubic units, such as cubic centimeters (cm³), cubic meters (m³), or cubic inches (in³). One cubic centimeter is a tiny cube that measures 1 cm on each side.
The Formula for Triangular Prism Volume
The formula to find the volume of a triangular prism is simple and straightforward: Volume=Base Area×Height (or Length)\text{Volume} = \text{Base Area} \times \text{Height (or Length)}Volume=Base Area×Height (or Length)
Here’s what each term means:
- Base Area: The area of the triangular face.
- Height (or Length): The distance between the two triangular bases.
Since the base is a triangle, you can find its area using the triangle area formula: Base Area=12×base×height of the triangle\text{Base Area} = \frac{1}{2} \times \text{base} \times \text{height of the triangle}Base Area=21×base×height of the triangle
So, the full formula for the triangular prism volume becomes: Volume=12×base×height of triangle×length of prism\text{Volume} = \frac{1}{2} \times \text{base} \times \text{height of triangle} \times \text{length of prism}Volume=21×base×height of triangle×length of prism
Step-by-Step Example: How to Calculate Triangular Prism Volume
Let’s look at a simple example to understand how this works.
Example:
A triangular prism has:
- A triangle base with a base of 8 cm
- A triangle height of 5 cm
- A prism length of 12 cm
Step 1: Find the base area.
Base area = ½ × 8 × 5 = 20 cm²
Step 2: Multiply by the prism’s length.
Volume = 20 × 12 = 240 cm³
Answer:
The triangular prism volume is 240 cubic centimeters.
That’s it! Just two steps, and you’re done.
Real-Life Examples of Triangular Prisms
You might be surprised to learn that triangular prisms are everywhere around us. Here are a few examples:
- A camping tent shaped like a triangle on both ends.
- The roof of a house, if it has a triangular cross-section.
- A Toblerone chocolate bar — one of the tastiest triangular prisms!
- Certain bridges and ramps that use triangular supports.
In all these cases, knowing the volume of a triangular prism can help in real-life applications like construction, packaging, and design.
Why Knowing Volume Matters
Understanding how to calculate triangular prism volume isn’t just for math class. It’s useful in many fields, such as:
- Architecture and Engineering: To know how much material is needed to build a roof or structure.
- Manufacturing: To estimate how much space a product occupies.
- Everyday Life: To find out how much a container or tank can hold.
Volume is all about space and capacity, and once you master it, you’ll find it’s a skill you can use often.
Common Mistakes When Finding Triangular Prism Volume
Even though the formula is simple, people sometimes make small mistakes. Let’s look at a few common ones and how to avoid them.
- Mixing up the triangle height and prism length.
The triangle height is part of the triangle’s base area, not the prism’s length. - Forgetting to divide by two.
Always remember that the triangle area formula includes ½. - Using different units.
Make sure all your measurements use the same unit (cm, m, or in). - Rounding too early.
Always calculate completely before rounding your final answer.
Avoiding these errors will keep your work accurate and easy.
Visualizing a Triangular Prism
If you have trouble picturing what’s happening, try drawing it. Sketch two triangles and connect their corners with rectangles. That’s your prism!
Visualizing helps you see which part is the base, which part is the height, and how the length connects the two triangles. This makes the triangular prism volume formula easier to understand and remember.
Different Types of Triangular Prisms
Not all triangular prisms are the same. Here are a few types you may see:
- Right Triangular Prism:
The triangular base has a right angle. It’s the most common and easiest to calculate. - Oblique Triangular Prism:
The sides are slanted, meaning the triangles aren’t directly above each other. The formula still works, but you must use the perpendicular distance between the triangles for length. - Regular Triangular Prism:
The triangular base is an equilateral triangle (all sides are equal).
No matter which type you have, you can still use the same triangular prism volume formula—it’s universal!
How to Find Missing Measurements
Sometimes, not all measurements are given. Here’s how to handle that:
- If the triangle base or height is missing, use geometry rules like the Pythagorean theorem.
- If the volume is given and you need to find length, rearrange the formula: Length=VolumeBase Area\text{Length} = \frac{\text{Volume}}{\text{Base Area}}Length=Base AreaVolume
- Always write down what you know first before solving.
With a little logic, you can always find the missing piece.
Using Units Correctly
When you work with volume, units matter a lot. If your base is in centimeters and your height in meters, the answer won’t make sense. Always convert everything into the same unit before calculating.
Common units for volume include:
- Cubic centimeters (cm³)
- Cubic meters (m³)
- Cubic inches (in³)
- Cubic feet (ft³)
When you square or cube numbers, don’t forget to cube the units too. That keeps your answers clear and correct.
Practice Problems for You
Try solving these for fun:
- A triangular prism has a base of 6 cm, a height of 4 cm, and a length of 10 cm. What’s its volume?
- A prism has a triangular base area of 15 cm² and a length of 8 cm. Find the volume.
- The volume of a prism is 360 cm³, and its base area is 30 cm². Find the prism’s length.
Practicing helps you remember the formula and builds confidence in solving problems.
Fun Facts About Triangular Prisms
- A triangular prism always has five faces, nine edges, and six corners (vertices).
- Its cross-section is always a triangle, no matter where you cut it parallel to the base.
- In nature, crystals and rock formations often form prism-like shapes.
- Architects use triangular prisms for stability and style in buildings.
Understanding these little facts helps you appreciate how math shapes the world around us.
FAQs
1. What is the formula for the volume of a triangular prism?
The formula is: Volume=12×base×height of triangle×length of prism\text{Volume} = \frac{1}{2} \times \text{base} \times \text{height of triangle} \times \text{length of prism}Volume=21×base×height of triangle×length of prism
2. Can the triangular base be any kind of triangle?
Yes! The base can be right, equilateral, or scalene. Just find the area correctly for that type of triangle.
3. What units should I use for triangular prism volume?
Use cubic units like cm³, m³, or in³. Just make sure all measurements use the same unit before calculating.
4. How can I find the height of the triangle if it’s missing?
If you know the base and one of the other sides, use the Pythagorean theorem for right triangles, or the area formula rearranged to solve for height.
5. What’s the difference between a prism’s height and a triangle’s height?
The triangle’s height is inside the triangle. The prism’s height (or length) connects the two triangular faces. They’re not the same.
6. Why is it important to know triangular prism volume?
It helps in construction, packaging, design, and even in understanding everyday objects. Knowing volume helps you measure space, storage, and capacity accurately.
SAMS Odisha, short for the Student Academic Management System SAMS Odisha, is a state-level online portal designed to streamline admissions for various professional courses in Odisha. It provides a transparent and centralized system for students to apply, track, and manage their college admissions efficiently. Through SAMS Odisha, candidates can access real-time updates, seat availability, and counseling schedules, ensuring a smooth admission process. The portal is widely recognized for simplifying educational management across the state.
Conclusion
Congratulations! You now understand everything about triangular prism volume—from what it is to how to calculate it and where it’s used in real life. Remember, the formula is simple, but the concept is powerful. You can use it to measure, build, design, and understand the 3D world around you.
Next time you see a tent, roof, or candy bar shaped like a prism, you’ll know exactly how to find its volume. Keep practicing, stay curious, and keep exploring how math connects to the world around you!