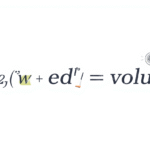Have you ever looked at a pyramid and wondered how much space is inside it? From the Great Pyramid of Giza to the tiny pyramids made for math class, these shapes are full of wonder. Today, we’ll learn everything you need to know about the volume of a pyramid — what it means, how to find it, and why it matters in real life.
This guide will make math feel simple and fun. You don’t need to be a genius to understand it. By the end, you’ll know how to find the volume of any pyramid, whether it’s square, triangular, or rectangular. Let’s begin our math adventure
Table of Contents
What Is the Volume of a Pyramid?
The volume of a pyramid is the amount of space inside it. Think of it like how much sand, water, or air could fit inside that shape. Every 3D object has volume — cubes, spheres, cylinders, and pyramids too.
A pyramid has a base (the bottom part) and triangular faces that meet at one point on top, called the apex. Because of this pointy top, a pyramid holds less space than a box with the same base and height.
To find the volume of a pyramid, we use a simple rule. It’s always one-third of the volume of a prism with the same base and height. That’s why the formula is:
Volume = (1/3) × Base Area × Height
This neat little formula works for all pyramids!
Why Is It One-Third?
You might wonder, “Why do we divide by three?” That’s a great question! Imagine filling a box and a pyramid that both have the same base and height. If you pour sand from the pyramid into the box, you’ll need three full pyramids to fill it completely.
That’s how mathematicians discovered that the volume of a pyramid is exactly one-third of its matching prism. This idea has been proven using geometry for centuries — and it never fails!
Understanding the Parts of a Pyramid
Before calculating anything, let’s know what each part means:
- Base: The flat bottom shape (square, rectangle, triangle, or other polygon).
- Height (h): The straight distance from the apex down to the center of the base.
- Slant Height: The diagonal line along the side of the pyramid — not used in volume but helpful in surface area.
- Apex: The top point where all faces meet.
Once you know the base area and height, you can easily find the volume using the formula.
The Formula for Volume of a Pyramid
Let’s write it again clearly: Volume of a Pyramid=13×Base Area×Height\text{Volume of a Pyramid} = \frac{1}{3} \times \text{Base Area} \times \text{Height}Volume of a Pyramid=31×Base Area×Height
This works for every type of pyramid. You just need to change the base area part depending on the shape of the base.
Volume of a Square Pyramid
A square pyramid has a square base. So, to find its volume:
- Find the area of the square base: Base Area=side2\text{Base Area} = \text{side}^2Base Area=side2
- Multiply by the height.
- Divide by 3.
Volume=13×s2×h\text{Volume} = \frac{1}{3} \times s^2 \times hVolume=31×s2×h
Example:
If the base side is 6 cm and the height is 9 cm:
Volume = (1/3) × 6² × 9 = (1/3) × 36 × 9 = 108 cm³.
So, the pyramid holds 108 cubic centimeters of space.
Volume of a Rectangular Pyramid
Some pyramids have rectangular bases. The rule is the same, but the base area is different. Volume=13×(l×w)×h\text{Volume} = \frac{1}{3} \times (l \times w) \times hVolume=31×(l×w)×h
Example:
A rectangular pyramid has a base 8 cm long, 5 cm wide, and height 12 cm.
Volume = (1/3) × (8 × 5) × 12 = (1/3) × 40 × 12 = 160 cm³.
Volume of a Triangular Pyramid
When the base is a triangle, the area formula changes slightly. Volume=13×(12×base×height of triangle)×pyramid height\text{Volume} = \frac{1}{3} \times \left(\frac{1}{2} \times \text{base} \times \text{height of triangle}\right) \times \text{pyramid height}Volume=31×(21×base×height of triangle)×pyramid height
Example:
If the triangular base has a base of 6 cm and a height of 4 cm, and the pyramid height is 9 cm:
Base area = (1/2 × 6 × 4) = 12 cm²
Volume = (1/3) × 12 × 9 = 36 cm³.
Real-Life Examples of Pyramid Volume
The volume of a pyramid isn’t just for math class. It shows up in real life all the time. Architects, engineers, and builders use it when designing roofs, monuments, and buildings.
For example:
- Builders might calculate how much concrete to pour for a pyramid-shaped roof.
- Artists use it when making pyramid sculptures or chocolate molds.
- Archaeologists estimate the volume of ancient pyramids to guess how many blocks were used.
Even in games like Minecraft or LEGO building, understanding pyramid volume helps make realistic structures!
How to Find the Base Area Easily
The base area depends on the shape of the pyramid’s bottom. Here are some quick tricks:
- Square base: side × side
- Rectangle base: length × width
- Triangle base: ½ × base × height
- Pentagon or hexagon base: use given formulas or divide into triangles
Once you know the area, plug it into the main volume formula. Easy!
Step-by-Step Guide to Finding the Volume of a Pyramid
Let’s put it all together in simple steps:
- Identify the base shape. (Square, rectangle, or triangle.)
- Find the area of the base.
- Measure the height from the center of the base to the apex.
- Multiply the base area by the height.
- Divide by 3.
That’s it! You’ve found the volume of a pyramid.
Fun Fact: The Great Pyramid of Giza
The Great Pyramid of Giza is one of the oldest and largest pyramids in the world. It’s about 230 meters wide at the base and 146 meters tall.
Using the formula:
Volume = (1/3) × (230²) × 146 ≈ 2,570,000,000 cubic meters!
That’s a lot of stone. This example shows how powerful the volume of a pyramid formula can be for huge structures.
Common Mistakes to Avoid
Many students make small mistakes when working with pyramid volume. Let’s fix them:
- Using slant height instead of height: Always use the vertical height (apex straight down to the base).
- Forgetting to divide by three: Remember, a pyramid is one-third of a prism.
- Mixing units: Keep all measurements in the same units (cm, m, etc.).
- Wrong base area: Double-check your base area calculation before multiplying.
Avoid these, and you’ll never go wrong with the volume of a pyramid again!
How Volume Changes With Size
If you double the height of a pyramid, the volume of the pyramid also doubles. But if you double the base length, the volume grows much faster!
This happens because the base area depends on two sides. So, making the pyramid taller or wider changes how much space it holds. That’s why builders carefully measure every part before construction.
Using the Volume Formula in Everyday Life
Even if you’re not an engineer, you can use this formula in fun ways.
- Making sandcastles shaped like pyramids? Estimate how much sand you need!
- Baking a pyramid cake? Measure its ingredients by volume.
- Designing in 3D software? The volume of a pyramid helps you get proportions right.
Learning this formula makes you see shapes differently — not just as flat drawings, but as real objects with depth.
Advanced Tip: Volume of a Frustum (Cut Pyramid)
Sometimes pyramids are sliced at the top. This creates a frustum, which also has a formula: V=13h(B1+B2+B1B2)V = \frac{1}{3}h(B_1 + B_2 + \sqrt{B_1B_2})V=31h(B1+B2+B1B2)
where B1B_1B1 and B2B_2B2 are the base areas of the top and bottom, and hhh is the height.
This is a fun extension once you’ve mastered the basic volume of a pyramid.
FAQs
1. What is the formula for the volume of a pyramid?
The formula is Volume = (1/3) × Base Area × Height. This rule works for all pyramids.
2. Why is the volume one-third of a prism?
Because it takes three pyramids of the same base and height to fill one prism completely.
3. What units are used for pyramid volume?
Volume is measured in cubic units — like cubic centimeters (cm³), cubic meters (m³), or cubic inches (in³).
4. Can the base be any shape?
Yes! The base can be a square, rectangle, triangle, pentagon, or even a hexagon.
5. What’s the difference between slant height and height?
Height is vertical (straight down). Slant height is diagonal along the side. For volume, always use the vertical height.
6. How do I find the volume if I only know the side length and slant height?
You can use the Pythagorean theorem to find the vertical height first, then use the volume formula.
Wrapping It Up: Why the Volume of a Pyramid Matters
Now you know everything about the volume of a pyramid — from its simple formula to its amazing real-world uses.
This topic isn’t just about math. It teaches how shapes work in real life, from ancient wonders to modern buildings. Every time you see a pyramid, you’ll know exactly how much space is hidden inside.
Remember:
Volume = (1/3) × Base Area × Height
Next time you’re in math class, building a model, or exploring geometry, try calculating the volume yourself. It’s a fun way to turn numbers into something real and meaningful!